Images fractales – audio ogg= »http://frank-lovisolo.fr/cat/ogg/Julia-Mandelbleu.ogg » audio mp3= »http://frank-lovisolo.fr/cat/m3p/Julia-Mandelbleu.mp3″ width= »280″ height= »40″ autoplay= »true » loop= »true »
 |
 à l’écoute : Julia MandelBleu |
  Zn+1 = Zn2 + c … et quelques bricoles !avec : Benoît Mandelbrot – Pierre Fatou – Gaston Julia – Adrien Douady –
et beaucoup d’autres…
|
|
Exposition virtuelle d’art numérique. |
|
|
|
|
|
|
Images fractales : l’atelier !!!–
Là, exceptionnellement, et sans que ça se reproduise trop souvent, je vous donnerai raison ! Cependant, vous serez obligé de reconnaître, à votre tour, qu’un pinceau et de la couleur ne sont pas très novateurs! Pour l’illustration du précédent article, Le Sanctuaire Des Nombres, j’ai dû explorer un nouveau chemin. Je n’étais pas satisfait par ce que je pouvais obtenir uniquement avec la photographie… Dès lors, en route pour un autre univers; celui du Mandelbulb1 qui résulte d’un ensemble de Mandelbrot en trois dimensions.
Ce n’est rien de le dire !
Daniel White et Paul Nylander ont construit un «Mandelbulb», un analogue en dimension 3 de l’ensemble de Mandelbrot, à l’aide d’une algèbre de nombres hypercomplexes et de transformations écrites en coordonnées sphériques. ( Fastoche, non? 🙂 ) White et Nylander nous donnent la formule suivante :
( celle -là, vous ne l’avez pas volée !!! )  L’éponge de Menger un peu bricolée!!!  Yves Klein – SE 71, L’Arbre, grande éponge bleue – 1962 Jolie formule, un tantinet hermétique, qui va, à l’aide d’un programme idoine, me permettre de réaliser les tableaux de cette exposition virtuelle: La galerie « Julia Mandelbleu ». Il s’agit du logiciel «Mandelbulb3D» développé par Jesse et un groupe de contributeurs à « Fractals Forums » que je ne saurai que trop remercier ! Pour cette virtuelle exposition, j’ai eu le désir d’une représentation graphique plus éloignée des images que l’on pourrait qualifier de «traditionnelles» dans cette discipline et me rapprocher d’une inspiration limitrophe à une branche de l’art contemporain que l’on pourrait, de nos jours, qualifier de classique… Par exemple, il n’est pas inconcevable de faire un parallèle entre l’éponge d’Yves Klein et celle de Karl Menger ! (Voir ici le répertoire) Quant au bleu… Ce ne sera pas la première fois : en 2012, ces quelques coups de pinceau d’une personne qui avait essuyé le sien sur l’armature blanche d’un l’escalier.
Éphémères, ces quelques tâches poétiquement bleues à l’entretien d’icelui s’en sont allées…
Sur le port Saint-Louis du Mourillon à Toulon: l’article «Bleues Éphémères». |
Vue de l’atelier numérique
|
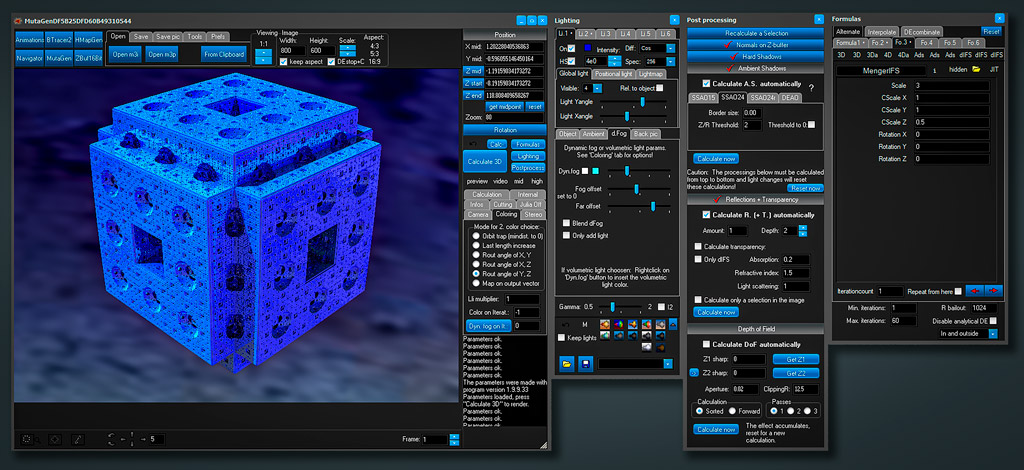 L’éponge de Menger, ou éponge de Menger-Sierpinski, en construction avec de nouveaux paramètres. |
 Cyanomètre de 1789 pour évaluer le bleu du ciel TechniquesToutes sortes de fractales ont été utilisées comme base pour l’art numérique. Des images colorées en haute qualité graphique sont devenues de plus en plus accessibles dans les laboratoires de recherche scientifique dans les années 1980. Des formes d’art scientifique, comme l’art fractal, se sont développées séparément de la culture dominante. En commençant par des images montrant les détails de fractales bidimensionnelles comme l’ensemble de Mandelbrot, les fractales ont trouvé des applications artistiques dans de nombreux domaines, aussi variés de la génération de texture, la simulation de pousse de plante et la génération de paysages. Les fractales sont parfois combinées avec des algorithmes évolutionnistes, soit en choisissant itérativement des spécimens jugés beaux dans un ensemble de variation aléatoire d’une œuvre fractale et en produisant ensemble de nouvelles variations, pour éviter d’obtenir des résultats incertains ou peu satisfaisants, ou collectivement, comme dans le projet Electric Sheep, où les gens utilisent des flammes fractales réalisées grâce au calcul distribué comme écran de veille. Ils peuvent ensuite « noter » les flammes fractales qu’ils voient et ces notes influencent le serveur qui adapte l’algorithme pour réduire les chances d’obtenir des flammes fractales jugées indésirables et augmenter les chances d’obtenir des flammes fractales désirables. Ce projet est donc une œuvre d’art générée par ordinateur et créée par une communauté entière. Beaucoup de ces images sont admirées pour l’harmonie que les gens y perçoivent. Ce résultat est souvent réussi grâce aux motifs émergeant de l’équilibre entre ordre et chaos. Des qualités similaires ont été décrites dans les peintures chinoises et les penjings. |
| https://fr.wikipedia.org/wiki/Mandelbulb –Mandelbulb3D v199sr33 |
|
Pour l’exposition de la galerie de l’école de design ESDAC, «Un art déconfiné».
Quelques sources d’inspirations bleutées. |
|
 Rothko Mark Peinture, 1956, 228.6×161.3 cm  Yves Klein – SE 71, L’Arbre, grande éponge bleue – 1962  La Nuit étoilée – Vincent Van Gogh – 25 mai 1889  Bleu II – Joan Miró – 1961  Pierre Soulages (N. 1919), Peinture 81 x 130 cm  Jesús Rafael Soto – Cube bleu interne – 1976  Anish Kapoor – Dragon, 1992 |
Palette de teintes de bleu avec leurs noms…
| 1- Jos Leys, « MANDELBULB » [archive], sur images.math.cnrs.fr. |
|
|
| Signaler un problème – Report a problem |
[lwptoc title= »Table des matières – Contents » toggle= »1″ hideItems= »1″ width= »460px » float= »center » colorScheme= »light » hoverLinkColor= »#dd0000″ skipHeadingText= » »] |
On y voit que du bleu !!! Expression mal venue pou ces artistes. musicalement bleu je veux dire beau.
Le bleu est une couleur qui sied à notre région, on peut s’y soustraire. Il est soit en haut soit en bas… Merci !!!!
Un moment de détente en lisant ce billet et en écoutant la musique associée. Je me suis abonnée à votre page twitter.
Je vous remercie beaucoup !!!